Comma category

In mathematics, a comma category (a special case being a slice category) is a construction in category theory. It provides another way of looking at morphisms: instead of simply relating objects of a category to one another, morphisms become objects in their own right. This notion was introduced in 1963 by F. W. Lawvere (Lawvere, 1963 p. 36), although the technique did not become generally known until many years later. Several mathematical concepts can be treated as comma categories. Comma categories also guarantee the existence of some limits and colimits. The name comes from the notation originally used by Lawvere, which involved the comma punctuation mark. The name persists even though standard notation has changed, since the use of a comma as an operator is potentially confusing, and even Lawvere dislikes the uninformative term "comma category" (Lawvere, 1963 p. 13).

Definition

The most general comma category construction involves two functors with the same codomain. Often one of these will have domain 1 (the one-object one-morphism category). Some accounts of category theory consider only these special cases, but the term comma category is actually much more general.

General form

Suppose that ${\mathcal {A}}$, ${\mathcal {B}}$, and ${\mathcal {C}}$ are categories, and $S$ and $T$ (for source and target) are functors:

${\mathcal {A}}{\xrightarrow {\;\;S\;\;}}{\mathcal {C}}{\xleftarrow {\;\;T\;\;}}{\mathcal {B}}$

We can form the comma category $(S\downarrow T)$ as follows:

• The objects are all triples $(A,B,h)$ with $A$ an object in ${\mathcal {A}}$, $B$ an object in ${\mathcal {B}}$, and $h:S(A)\rightarrow T(B)$ a morphism in ${\mathcal {C}}$.
• The morphisms from $(A,B,h)$ to $(A',B',h')$ are all pairs $(f,g)$ where $f:A\rightarrow A'$ and $g:B\rightarrow B'$ are morphisms in ${\mathcal {A}}$ and ${\mathcal {B}}$ respectively, such that the following diagram commutes:

Comma Diagram

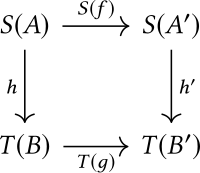
Morphisms are composed by taking $(f',g')\circ (f,g)$ to be $(f'\circ f,g'\circ g)$, whenever the latter expression is defined. The identity morphism on an object $(A,B,h)$ is $(\mathrm {id} _{A},\mathrm {id} _{B})$.

Slice category

Main article: Overcategory

The first special case occurs when ${\mathcal {C}}={\mathcal {A}}$, the functor $S$ is the identity functor, and ${\mathcal {B}}={\textbf {1}}$ (the category with one object $*$ and one morphism). Then $T(*)=A_{*}$ for some object $A_{*}$ in ${\mathcal {A}}$.

${\mathcal {A}}\xrightarrow {\;\;\mathrm {id} _{\mathcal {A}}\;\;} {\mathcal {A}}\xleftarrow {\;\;A_{*}\;\;} {\textbf {1}}$

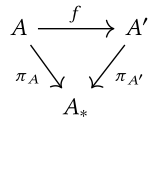
In this case, the comma category is written $({\mathcal {A}}\downarrow A_{*})$, and is often called the slice category over $A_{*}$ or the category of objects over $A_{*}$. The objects $(A,*,h)$ can be simplified to pairs $(A,h)$, where $h:A\rightarrow A_{*}$. Sometimes, $h$ is denoted by $\pi _{A}$. A morphism $(f,\mathrm {id} _{*})$ from $(A,\pi _{A})$ to $(A',\pi _{A'})$ in the slice category can then be simplified to an arrow $f:A\rightarrow A'$ making the following diagram commute:

Slice Diagram

Coslice category

Main article: Overcategory

The dual concept to a slice category is a coslice category. Here, ${\mathcal {C}}={\mathcal {B}}$, $S$ has domain ${\textbf {1}}$ and $T$ is an identity functor.

${\textbf {1}}\xrightarrow {\;\;B_{*}\;\;} {\mathcal {B}}\xleftarrow {\;\;\mathrm {id} _{\mathcal {B}}\;\;} {\mathcal {B}}$

In this case, the comma category is often written $(B_{*}\downarrow {\mathcal {B}})$, where $B_{*}=S(*)$ is the object of ${\mathcal {B}}$ selected by $S$. It is called the coslice category with respect to $B_{*}$, or the category of objects under $B_{*}$. The objects are pairs $(B,\iota _{B})$ with $\iota _{B}:B_{*}\rightarrow B$. Given $(B,\iota _{B})$ and $(B',\iota _{B'})$, a morphism in the coslice category is a map $g:B\rightarrow B'$ making the following diagram commute:

Coslice Diagram

Arrow category

$S$ and $T$ are identity functors on ${\mathcal {C}}$ (so ${\mathcal {A}}={\mathcal {B}}={\mathcal {C}}$).

${\mathcal {C}}\xrightarrow {\;\;\mathrm {id} _{\mathcal {C}}\;\;} {\mathcal {C}}\xleftarrow {\;\;\mathrm {id} _{\mathcal {C}}\;\;} {\mathcal {C}}$

In this case, the comma category is the arrow category ${\mathcal {C}}^{\rightarrow }$. Its objects are the morphisms of ${\mathcal {C}}$, and its morphisms are commuting squares in ${\mathcal {C}}$.

Arrow Diagram

Other variations

In the case of the slice or coslice category, the identity functor may be replaced with some other functor; this yields a family of categories particularly useful in the study of adjoint functors. For example, if $T$ is the forgetful functor mapping an abelian group to its underlying set, and $s$ is some fixed set (regarded as a functor from 1), then the comma category $(s\downarrow T)$ has objects that are maps from $s$ to a set underlying a group. This relates to the left adjoint of $T$, which is the functor that maps a set to the free abelian group having that set as its basis. In particular, the initial object of $(s\downarrow T)$ is the canonical injection $s\rightarrow T(G)$, where $G$ is the free group generated by $s$.

An object of $(s\downarrow T)$ is called a morphism from $s$ to $T$ or a $T$-structured arrow with domain $s$. An object of $(S\downarrow t)$ is called a morphism from $S$ to $t$ or a $S$-costructured arrow with codomain $t$.

Another special case occurs when both $S$ and $T$ are functors with domain ${\textbf {1}}$. If $S(*)=A$ and $T(*)=B$, then the comma category $(S\downarrow T)$, written $(A\downarrow B)$, is the discrete category whose objects are morphisms from $A$ to $B$.

An inserter category is a (non-full) subcategory of the comma category where ${\mathcal {A}}={\mathcal {B}}$ and $f=g$ are required. The comma category can also be seen as the inserter of $S\circ \pi _{1}$ and $T\circ \pi _{2}$, where $\pi _{1}$ and $\pi _{2}$ are the two projection functors out of the product category ${\mathcal {A}}\times {\mathcal {B}}$.

Properties

For each comma category there are forgetful functors from it.

• Domain functor, $S\downarrow T\to {\mathcal {A}}$, which maps:
  • objects: $(A,B,h)\mapsto A$;
  • morphisms: $(f,g)\mapsto f$;
• Codomain functor, $S\downarrow T\to {\mathcal {B}}$, which maps:
  • objects: $(A,B,h)\mapsto B$;
  • morphisms: $(f,g)\mapsto g$.
• Arrow functor, $S\downarrow T\to {\mathcal {C}}^{\rightarrow }$, which maps:
  • objects: $(A,B,h)\mapsto h$;
  • morphisms: $(f,g)\mapsto (Sf,Tg)$;

Examples of use

Some notable categories

Several interesting categories have a natural definition in terms of comma categories.

• The category of pointed sets is a comma category, $\scriptstyle {(\bullet \downarrow \mathbf {Set} )}$ with $\scriptstyle {\bullet }$ being (a functor selecting) any singleton set, and $\scriptstyle {\mathbf {Set} }$ (the identity functor of) the category of sets. Each object of this category is a set, together with a function selecting some element of the set: the "basepoint". Morphisms are functions on sets which map basepoints to basepoints. In a similar fashion one can form the category of pointed spaces $\scriptstyle {(\bullet \downarrow \mathbf {Top} )}$.
• The category of associative algebras over a ring $R$ is the coslice category $\scriptstyle {(R\downarrow \mathbf {Ring} )}$, since any ring homomorphism $f:R\to S$ induces an associative $R$-algebra structure on $S$, and vice versa. Morphisms are then maps $h:S\to T$ that make the diagram commute.
• The category of graphs is $\scriptstyle {(\mathbf {Set} \downarrow D)}$, with $\scriptstyle {D:\,\mathbf {Set} \rightarrow \mathbf {Set} }$ the functor taking a set $s$ to $s\times s$. The objects $(a,b,f)$ then consist of two sets and a function; $a$ is an indexing set, $b$ is a set of nodes, and $f:a\rightarrow (b\times b)$ chooses pairs of elements of $b$ for each input from $a$. That is, $f$ picks out certain edges from the set $b\times b$ of possible edges. A morphism in this category is made up of two functions, one on the indexing set and one on the node set. They must "agree" according to the general definition above, meaning that $(g,h):(a,b,f)\rightarrow (a',b',f')$ must satisfy $f'\circ g=D(h)\circ f$. In other words, the edge corresponding to a certain element of the indexing set, when translated, must be the same as the edge for the translated index.
• Many "augmentation" or "labelling" operations can be expressed in terms of comma categories. Let $S$ be the functor taking each graph to the set of its edges, and let $A$ be (a functor selecting) some particular set: then $(S\downarrow A)$ is the category of graphs whose edges are labelled by elements of $A$. This form of comma category is often called objects $S$-over $A$ - closely related to the "objects over $A$" discussed above. Here, each object takes the form $(B,\pi _{B})$, where $B$ is a graph and $\pi _{B}$ a function from the edges of $B$ to $A$. The nodes of the graph could be labelled in essentially the same way.
• A category is said to be locally cartesian closed if every slice of it is cartesian closed (see above for the notion of slice). Locally cartesian closed categories are the classifying categories of dependent type theories.

Limits and universal morphisms

Limits and colimits in comma categories may be "inherited". If ${\mathcal {A}}$ and ${\mathcal {B}}$ are complete, $T:{\mathcal {B}}\rightarrow {\mathcal {C}}$ is a continuous functor, and $S\colon {\mathcal {A}}\rightarrow {\mathcal {C}}$ is another functor (not necessarily continuous), then the comma category $(S\downarrow T)$ produced is complete, and the projection functors $(S\downarrow T)\rightarrow {\mathcal {A}}$ and $(S\downarrow T)\rightarrow {\mathcal {B}}$ are continuous. Similarly, if ${\mathcal {A}}$ and ${\mathcal {B}}$ are cocomplete, and $S:{\mathcal {A}}\rightarrow {\mathcal {C}}$ is cocontinuous, then $(S\downarrow T)$ is cocomplete, and the projection functors are cocontinuous.

For example, note that in the above construction of the category of graphs as a comma category, the category of sets is complete and cocomplete, and the identity functor is continuous and cocontinuous. Thus, the category of graphs is complete and cocomplete.

The notion of a universal morphism to a particular colimit, or from a limit, can be expressed in terms of a comma category. Essentially, we create a category whose objects are cones, and where the limiting cone is a terminal object; then, each universal morphism for the limit is just the morphism to the terminal object. This works in the dual case, with a category of cocones having an initial object. For example, let ${\mathcal {C}}$ be a category with $F:{\mathcal {C}}\rightarrow {\mathcal {C}}\times {\mathcal {C}}$ the functor taking each object $c$ to $(c,c)$ and each arrow $f$ to $(f,f)$. A universal morphism from $(a,b)$ to $F$ consists, by definition, of an object $(c,c)$ and morphism $\rho :(a,b)\rightarrow (c,c)$ with the universal property that for any morphism $\rho ':(a,b)\rightarrow (d,d)$ there is a unique morphism $\sigma :c\rightarrow d$ with $F(\sigma )\circ \rho =\rho '$. In other words, it is an object in the comma category $((a,b)\downarrow F)$ having a morphism to any other object in that category; it is initial. This serves to define the coproduct in ${\mathcal {C}}$, when it exists.

Adjunctions

William Lawvere showed that the functors $F:{\mathcal {C}}\rightarrow {\mathcal {D}}$ and $G:{\mathcal {D}}\rightarrow {\mathcal {C}}$ are adjoint if and only if the comma categories $(F\downarrow id_{\mathcal {D}})$ and $(id_{\mathcal {C}}\downarrow G)$, with $id_{\mathcal {D}}$ and $id_{\mathcal {C}}$ the identity functors on ${\mathcal {D}}$ and ${\mathcal {C}}$ respectively, are isomorphic, and equivalent elements in the comma category can be projected onto the same element of ${\mathcal {C}}\times {\mathcal {D}}$. This allows adjunctions to be described without involving sets, and was in fact the original motivation for introducing comma categories.

Natural transformations

If the domains of $S,T$ are equal, then the diagram which defines morphisms in $S\downarrow T$ with $A=B,A'=B',f=g$ is identical to the diagram which defines a natural transformation $S\to T$. The difference between the two notions is that a natural transformation is a particular collection of morphisms of type of the form $S(A)\to T(A)$, while objects of the comma category contains all morphisms of type of such form. A functor to the comma category selects that particular collection of morphisms. This is described succinctly by an observation by S.A. Huq that a natural transformation $\eta :S\to T$, with $S,T:{\mathcal {A}}\to {\mathcal {C}}$, corresponds to a functor ${\mathcal {A}}\to (S\downarrow T)$ which maps each object $A$ to $(A,A,\eta _{A})$ and maps each morphism $f=g$ to $(f,g)$. This is a bijective correspondence between natural transformations $S\to T$ and functors ${\mathcal {A}}\to (S\downarrow T)$ which are sections of both forgetful functors from $S\downarrow T$.

References

• Comma category at the nLab
• Lawvere, W (1963). "Functorial semantics of algebraic theories" and "Some algebraic problems in the context of functorial semantics of algebraic theories". http://www.tac.mta.ca/tac/reprints/articles/5/tr5.pdf

External links

• J. Adamek, H. Herrlich, G. Stecker, Abstract and Concrete Categories-The Joy of Cats
• Interactive Web page which generates examples of categorical constructions in the category of finite sets.